There are
several methods used to value companies and their stocks. They
attempt to give an estimate of their fair value, by using fundamental
economic criteria. This theoretical valuation has to be perfected
with market criteria, as the final purpose is to determine potential
market prices.
Fundamental
criteria (fair value)
The most
theoretically sound stock valuation method is called
income valuation or the discounted cash flow (DCF) method,
involving discounting the profits (dividends, earnings,
or cash flows) the stock will bring to the stockholder in the
foreseeable future, and a final value on disposition. The discount
rate normally has to include a risk premium which is commonly
based on the capital asset pricing model.
Approximate
valuation approaches
Average
growth approximation: Assuming that two stocks have the
same earnings growth, the one with a lower P/E is a better value.
The P/E method is perhaps the most commonly used valuation method
in the stock brokerage industry. By using comparison firms,
a target price/earnings (or P/E) ratio is selected for the company,
and then the future earnings of the company are estimated. The
valuation's fair price is simply estimated earnings times target
P/E. This model is essentially the same model as Gordon's model,
if k-g is estimated as the dividend payout ratio (D/E) divided
by the target P/E ratio.
Constant growth approximation: The Gordon model or Gordon's
growth model[1]
is the best known of a class of discounted dividend models.
It assumes that dividends will increase at a constant growth
rate (less than the discount rate) forever. The valuation is
given by the formula:
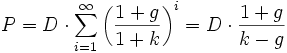 .
.
and the
following table defines each symbol:
| Symbol |
Meaning |
Units |
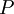 |
estimated stock price |
$ or € or £ |
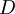 |
last dividend paid |
$ or € or £ |
 |
discount rate |
% |
 |
the growth rate of the dividends |
% |
[1]
Limited
high-growth period approximation: When a stock has a significantly
higher growth rate than its peers, it is sometimes assumed that
the earnings growth rate will be sustained for a short time
(say, 5 years), and then the growth rate will revert to the
mean. This is probably the most rigorous approximation that
is practical [2].
Market
criteria (potential price)
Some feel
that if the stock is listed in a well organized stock market,
with a large volume of transactions, the listed price will be
close to the estimated fair value. This is called the efficient market hypothesis.
On the other
hand, studies made in the field of behavioral finance tend to
show that deviations from the fair price are rather common,
and sometimes quite large.
Thus, in
addition to fundamental economic criteria, market criteria also
have to be taken into account market-based valuation. Valuing
a stock is not only to estimate its fair value, but also to
determine its potential price range, taking into account
market behavior aspects. One of the behavioral valuation tools
is the stock image, a coefficient that bridges the theoretical
fair value and the market price.
On-line
valuation calculators
References
External
links

