An
interest rate cap is a derivative in which the buyer receives money
at the end of each period in which an interest rate exceeds
the agreed strike price. An example of a cap would be an agreement
to receive money for each month the LIBOR rate exceeds 2.5%.
The interest
rate cap can be analyzed as a series of European call options
or caplets which exists for each period the cap agreement
is in existence.
In formulas
a caplet payoff on a rate L struck at K is
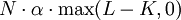
where N
is the notional value exchanged and α is the day count fraction corresponding to the period
to which L applies. For example suppose you own a caplet on
the six month USD LIBOR rate with an expiry of 1st February
2007 struck at 2.5% with a notional of 1 million dollars. Then
if the USD LIBOR rate sets at 3% on 1st February you receive
1m*0.5*max(0.03-0.025,0) = $2500. Customarily the payment is
made at the end of the rate period, in this case on 1st August.
Interest
rate floor
An interest
rate floor is a series of European put options or floorlets
on a specified reference rate, usually LIBOR. The buyer of the
floor receives money if on the maturity of any of the floorlets,
the reference rate fixed is below the agreed strike price of
the floor.
Valuation
of interest rate caps
Black
Model
The simplest
and most common valuation of interest rate caplets is via the
Black model.
As
a bond put
It can be
shown that a cap on a LIBOR from t to T is equivalent
to a multiple of a t-maturity put on a T-maturity
bond. Thus if we have an interest rate model in which we are
able to value bond puts, we can value interest rate caps. Similarly
a floor is equivalent to a certain bond call. Several popular
short rate models, such as the Hull-White model have this degree
of tractability. Thus we can value caps and floors in those
models..
What
about Collars?
Interest
rate collar
¦the simultaneous
purchase of an interest rate cap and sale of an interest rate
floor on the same index for the same maturity and notional principal
amount
-
- The
cap rate is set above the floor rate.
- The objective
of the buyer of a collar is to protect against rising interest
rates.
- The
purchase of the cap protects against rising rates while
the sale of the floor generates premium income.
- A collar
creates a band within which the buyer’s effective interest
rate fluctuates
And
Reverse Collars?
…buying
an interest rate floor and simultaneously selling an interest
rate cap.
- The objective
is to protect the bank from falling interest rates.
- The buyer
selects the index rate and matches the maturity and notional
principal amounts for the floor and cap.
- Buyers
can construct zero cost reverse collars when it is possible
to find floor and cap rates with the same premiums that provide
an acceptable band.
The size
of cap and floor premiums are determined by a wide range of
factors
- The relationship
between the strike rate and the prevailing 3-month LIBOR
- premiums
are highest for in the money options and lower for at
the money and out of the money options
- Premiums
increase with maturity.
- The
option seller must be compensated more for committing
to a fixed-rate for a longer period of time.
- Prevailing
economic conditions, the shape of the yield curve, and the
volatility of interest rates.
- upsloping
yield curve -- caps will be more expensive than floors.
- the
steeper is the slope of the yield curve, ceteris paribus,
the greater are the cap premiums.
- floor
premiums reveal the opposite relationship. ]
Implied Volatilities
- An important
consideration is cap and floor volatilities. Caps consist
of caplets with volatilities dependent on the corresponding
forward LIBOR rate. But caps can be represented by a "flat
volatility", so the net of the caplets still comes out to
be the same. (15%,20%,....,12%) ---> (16.5%,16.5%,....,16.5%)
-
- So
one cap can be priced at one vol.
-
- Another
important intuition is that caps and floors are duals.
Cap-Floor = Swap.
-
- Caps
and floors have the same implied vol too for a given strike.
Imagine
a cap with 20% and floor with 30%. Long cap, short floor gives
a swap with no vol. Now, interchange the vols. Cap price goes
up, floor price goes down. But the net price of the swap is
unchanged. So, if a cap has x vol, floor is forced to have x
vol else you have arbitrage.
Compare
External
links

