Forward Contracts

A forward contract is an agreement between two parties to buy or sell an asset (which can be of any kind) at a pre-agreed future point in time. Therefore, the trade date and delivery date are separated. It is used to control and hedge risk, for example currency exposure risk (e.g., forward contracts on USD or EUR) or commodity prices (e.g., forward contracts on oil).

One party agrees (obligated) to sell, the other to buy, for a forward price agreed in advance. In a forward transaction, no actual cash changes hands. If the transaction is collateralized, exchange of margin will take place according to a pre-agreed rule or schedule. Otherwise no asset of any kind actually changes hands, until the maturity of the contract.

The forward price of such a contract is commonly contrasted with the spot price, which is the price at which the asset changes hands (on the spot date, usually two business days). The difference between the spot and the forward price is the forward premium or forward discount.

A standardized forward contract that is traded on an exchange is called a futures contract.

Example of how the payoff of a forward contract works

Suppose that Bob wants to buy a house in one year's time. At the same time, suppose that Andy currently owns a $100,000 house that he wishes to sell in one year's time. Both parties could enter into a forward contract with each other. Suppose that they both agree on the sale price in one year's time of $104,000 (more below on why the sale price should be this amount). Andy and Bob have entered into a forward contract. Bob, because he is buying the underlying, is said to have entered a long forward contract. Conversely, Andy will have the short forward contract.

At the end of one year, suppose that the current market valuation of Andy's house is $110,000. Then, because Andy is obliged to sell to Bob for only $104,000, Bob will make a profit of $6,000. To see why this is so, one needs only to recognize that Bob can buy from Andy for $104,000 and immediately sell to the market for $110,000. Bob has made the difference in profit. In contrast, Andy has made a loss of $6,000.

Example of how forward prices should be agreed upon

Continuing on the example above, suppose now that the initial price of Andy's house is $100,000 and that Bob enters into a forward contract to buy the house one year from today. But since Andy knows that he can immediately sell for $100,000 and place the proceeds in the bank, he wants to be compensated for the delayed sale. Suppose that the risk free rate of return R (the bank rate) for one year is 4%. Then the money in the bank would grow to $104,000, risk free. So Andy would want at least $104,000 one year from now for the contract to be worthwhile for him - the opportunity cost will be covered.

Bob, as any other buyer would, will seek the lowest price he can for the contract - although as we've seen, there is an invisible lower limit of $104,000 that Andy will not go below. As a result, the contract price would be at least $104,000 or it will not happen at all.

Rational pricing

If $S t$ is the spot price of an asset at time $t$ , and $r$ is the continuously compounded rate, then the forward price must satisfy $F t, T = S t e r (T - t)$ .

To prove this, suppose not. Then we have two possible cases.

Case 1: Suppose that $F t, T > S t e r (T - t)$ . Then an investor can execute the following trades at time $t$ :

go to the bank and get a loan for $S t$ at the continuously compounded rate r;
with this money from the bank, buy one unit of stock for $S t$ ;
enter into one short forward contract costing 0. A short forward contract means that the investor owes the counterparty the stock at time $T$ .

The initial cost of the trades at the initial time sum to zero.

At time $T$ the investor can reverse the trades that was executed at time $t$ . Specifically, and mirroring the trades 1., 2. and 3. the investor

' repays the loan to the bank. The inflow to the investor is $- S t e r (T - t)$ ;
' sells the stock for $S T$ . The cash inflow to the investor is now $S T$ .
' settles the short forward contract by receiving $S T$ from the buyer; there is an inflow of funds to the investor of $F t, T - S T$ .

The sum of the inflows in 1.', 2.' and 3.' equals $F t, T - S t e r (T - t)$ , which by hypothesis, is positive. This is an arbitrage profit. Consequently, and assuming that the non-arbitrage condition holds, we have a contradiction. This is called a cash and carry arbitrage because you "carry" the stock until maturity.

Case 2: Suppose that $F t, T < S t e r (T - t)$ . Then an investor can do the reverse of what he has done above in case 1. But if you look at the convenience yield page, you will see that if there are finite stocks/inventory, the reverse cash and carry arbitrage is not always possible. It would depend on the elasticity of demand for forward contracts and such like.

Extensions to the forward pricing formula

Suppose that $FV T (X)$ is the time value of cash flows X at the contract expiration time $T$ . The forward price is then given by the formula:

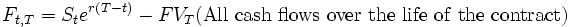
$F_{t,T} = S_t e^{r(T-t)} - FV_T(\mathrm{All\ cash\ flows\ over\ the\ life\ of\ the\ contract})$

The cash flows can be in the form of dividends from the asset, or costs of maintaining the asset.

If these price relationships do not hold, there is an arbitrage opportunity for a riskless profit similar to that discussed above. One implication of this is that the presence of a forward market will force spot prices to reflect current expectations of future prices. As a result, the forward price for nonperishable commodities, securities or currency is no more a predictor of future price than the spot price is - the relationship between forward and spot prices is driven by interest rates. For perishable commodities, arbitrage does not have this

The above forward pricing formula can also be written as:

F t, T = (S t - I t) e r (T - t)

Where $I t$ is the time t value of all cash flows over the life of the contract.

Theories of why a forward contract exists

Allaz and Vila (1993) suggest that there is also a strategic reason (in an imperfect competitive environment) for the existence of forward trading, that is, forward trading can be used even in a world without uncertainty. This is due to firms having Stackelberg incentives to anticipate their production through forward contracts.

See also

References

John C. Hull, (2000), Options, Futures and other Derivatives, Prentice-Hall.
Keith Redhead, (31 Oct 1996), Financial Derivatives: An Introduction to Futures, Forwards, Options and Swaps, Prentice-Hall
Abraham Lioui & Patrice Poncet, (March 30, 2005), Dynamic Asset Allocation with Forwards and Futures, Springer

Further reading

Allaz, B. and Vila, J.-L., Cournot competition, futures markets and efficiency, Journal of Economic Theory 59, 297-308.

All text is available under the terms of the GNU Free Documentation License (see Copyrights for details). Disclaimers. Wikipedia is powered by MediaWiki, an open source wiki engine.