Foreign Exchange Options

In finance, a foreign exchange option (commonly shortened to just FX option or currency option) is a derivative financial instrument where the owner has the right but not the obligation to exchange money denominated in one currency into another currency at a pre-agreed exchange rate on a specified date.

The FX options market is the deepest, largest and most liquid market for options of any kind in the world. Most of the FX option volume is traded OTC and is lightly regulated, but a fraction is traded on exchanges like the Philadelphia Stock Exchange, or the Chicago Mercantile Exchange for options on futures contracts: the global market for exchange-traded currency options is notionally valued by the Bank for International Settlements at $158,300 million in 2005.

Example

For example a GBPUSD FX option might be specified by a contract allowing the owner to sell £1,000,000 and buy $2,000,000 on December 31. In this case the pre-agreed exchange rate, or strike price, is 2.0000 GBPUSD or 0.5000 USDGBP and the notionals are £1,000,000 and $2,000,000 (£1,000,000 from the eyes of a USD investor, $2,000,000 from the eyes of a GBP investor).

This type of contract is both a call on dollars and a put on sterling, and is often called a GBPUSD put by market participants, as it is a put on the exchange rate; it could equally be called a USDGBP call, but isn't, as market convention is to quote the 2.0000 number (normal quote), not the 0.5000 number (inverse quote).

If the rate is lower than 2.0000 GBPUSD come December 31 (say at 1.9000 GBPUSD), meaning that the dollar is stronger and the pound is weaker, then the option will be exercised, allowing the owner to sell GBP at 2.0000 and immediately buy it back in the spot market at 1.9000, making a profit of (2.0000 USD/GBP - 1.9000 USD/GBP)*1,000,000 GBP = 100,000 USD in the process. If they immediately exchanges their profit into GBP, this amounts to 100,000/1.9000 = 52,631.58 GBP.

Terms

Generally in thinking about options, one assumes that one is buying an asset: for instance, you can have a call option on oil, which allows you to buy oil at a given price. One can consider this situation more symmetrically in FX, where one exchanges: a put on GBPUSD allows one to exchange GBP for USD: it is at once a put on GBP and a call on USD.

As a vivid example: people usually consider that in a fast food restaurant, one buys hamburgers and pays in dollars, but one can instead say that the restaurant buys dollars and pays in hamburgers.

There are a number of subtleties that follow from this symmetry.

Ratio of notionals: The ratio of the notionals in an FX option is the strike, not the current spot or forward. Notably, when constructing an option strategy from FX options, one must be careful to match the foreign currency notionals, not the local currency notionals, else the foreign currencies received and delivered don't offset and one is left with residual risk.
Non-linear payoff: The payoff for a vanilla option is linear in the underlying, when one denominates the payout in a given numeraire. In the case of an FX option on a rate, one must be careful of which currency is the underlying and which in the numeraire: in the above example, an option on GBPUSD gives a USD value that is linear in GBPUSD (a move from 2.0000 to 1.9000 yields a .10 * $2,000,000 / 2.0000 = $100,000 profit), but has a non-linear GBP value in GBPUSD. Conversely, the GBP value is linear in the USDGBP rate, while the USD value is non-linear in the USDGBP rate. This is because inverting a rate has the effect of 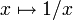$x \mapsto 1/x$ , which is non-linear.
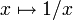Change of numeraire: the implied volatility of an FX option depends on the numéraire of the purchaser, again because of the non-linearity of $x \mapsto 1/x$ .

Hedging with FX options

Corporations primarily use FX options to hedge uncertain future cash flows in a foreign currency. The general rule is to hedge certain foreign currency cash flows with forwards, and uncertain foreign cash flows with options.

Suppose a United Kingdom manufacturing firm is expecting to be paid US$100,000 for a piece of engineering equipment to be delivered in 90 days. If the GBP strengthen against the US$ over the next 90 days the UK firm will lose money, as it will receive less GBP when the US$100,000 is converted into GBP. However, if the GBP weaken against the US$, then the UK firm will gain additional money: the firm is exposed to FX risk. Assuming that the cash flow is certain, the firm can enter into a forward contract to deliver the US$100,000 in 90 days time, in exchange for GBP at the current forward rate. This forward contract is free, and, presuming the expected cash arrives, exactly matches the firm's exposure, perfectly hedging their FX risk.

If the cash flow is uncertain, the firm will likely want to use options: if the firm enters a forward FX contract and the expected USD cash is not received, then the forward, instead of hedging, exposes the firm to FX risk in the opposite direction.

Using options, the UK firm can purchase a GBP call/USD put option (the right to sell part or all of their expected income for pounds sterling at a predetermined rate), which will:

protect the GBP value that the firm will receive in 90 day's time (presuming the cash is received)
cost at most the option premium (unlike a forward, which can have unlimited losses)
yield a profit if the expected cash is not received but FX rates move in its favor

Valuing FX options: The Garman-Kohlhagen model

As in the Black-Scholes model for stock options and the Black model for certain interest rate options, the value of an european option on a FX rate is typically calculated by assuming that the rate follows a log-normal process.

In 1983 Garman and Kohlhagen extended the Black-Scholes model to cope with the presence of two interest rates (one for each currency). Suppose that r_d is the risk-free interest rate to expiry of the domestic currency and r_f is the foreign currency risk-free interest rate (where domestic currency is the currency in which we obtain the value of the option; the formula also requires that FX rates - both strike and current spot be quoted in terms of "units of domestic currency per unit of foreign currency"). Then the domestic currency value of a call option into the foreign currency is

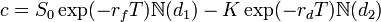
$c = S_0\exp(-r_f T)\N(d_1) - K\exp(-r_d T)\N(d_2)$

The value of a put option has value

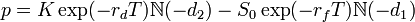
$p = K\exp(-r_d T)\N(-d_2) - S_0\exp(-r_f T)\N(-d_1)$

where :

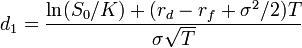
$d_1 = \frac{\ln(S_0/K) + (r_d - r_f + \sigma^2/2)T}{\sigma\sqrt{T}}$

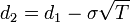
$d_2 = d_1 - \sigma\sqrt{T}$

S 0

is the current spot rate

K

is the strike price

N

is the cumulative normal distribution function

r d

is domestic risk free rate

r f

is foreign risk free rate

and

σ

is the volatility of the FX rate.

All text is available under the terms of the GNU Free Documentation License (see Copyrights for details). Disclaimers. Wikipedia is powered by MediaWiki, an open source wiki engine.