| |
|
In this lesson we will take a look at the 3-Dimensional world we live in. Look at the image below. You will see two points.
A line has only one dimension --length. The line has no endpoints and extends forever in both directions. That is why when a line is drawn, we see arrows at both ends. On the other hand when we draw a line segment on a piece of paper it has endpoints.
Question 1: How many endpoints does a line segment have?
Questions 2: What is the figure below called?
The line, ray and line segment are all examples of 1-Dimensional objects since they only have length.
On the other hand a square has both length and height.
Question 3: How many dimensions does a square have?
A square or rectangle is really a plane, a 2-Dimensional object that has no thickness.
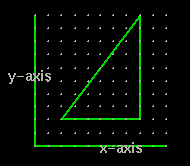
When we see a graph on a page we really don't think in terms of dimensions. But the graph above has only two axis or two dimensions. It is a plane.
Click
on Graph to see that it only has 2-D
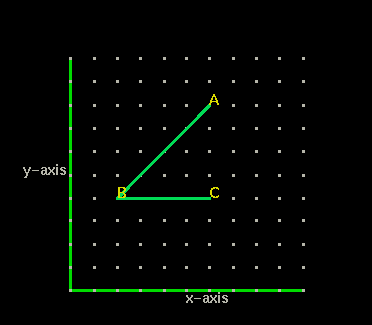
Point B has the coordinates (2,4). Starting from the origin (0,0) to reach point B we count 2 spaces to the right, then four spaces up.
Question 4: What are the coordinates of point A?
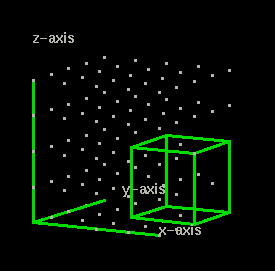
Compare the graph above (showing the cube) to the one shown in the above that contains angle ABC. What is different in this graph? Besides the x-axis and y-axis what do you see?
This graph has another axis, the z-axis. When we locate a point in three dimensions we need to use three coordinates. The origin in a two dimension plot is written (0,0).
Question 7: How do you write the coordinates for the origin in a 3-dimension plot?
What does all this have to do with molecules?
Look at the salt crystal structure above. Each atom is represented on the x,y,z coordinate axis as a single ball.
In the next section we will look at molecules and their relationship to mathematics.